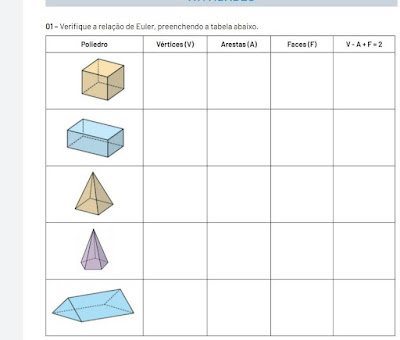
Verifique a relação de Euler, preenchendo a tabela abaixo.
Respostas
1.
Vamos verificar a validade aplicando a relação de Euler a cada poliedro.
A relação de Euler nos diz:
V – A + F = 2
onde V é o número de vértices, A é o número de arestas e F é o número de faces.
Vamos agora analisar cada poliedro na tabela.
Primeiro Poliedro:
O primeiro poliedro consiste em um cubo. Contamos 8 vértices (cada vértice corresponde a um dos “lados” do cubo).
Além disso, cada cubo tem 6 faces, 4 faces + 1 face inferior + 1 face superior. Também possui 12 arestas (cada uma correspondendo à parte linear do cubo).
Aplicação das relações de Euler:
V – A + F = 8-12 + 6 = 14-12 = 2
Segundo poliedro:
Tem um seixo vertical como um armário de sapatos normal. Novamente, podemos contar 8 vértices.
Tem 6 faces e 12 arestas. Seu valor é o mesmo do primeiro polidro.
Aplicação das relações de Euler:
V – A + F = 8-12 + 6 = 14-12 = 2
terceira foto:
Eu tenho uma pirâmide quadrada. Se você olhar para a foto, poderá contar 5 cabeças. (na parte inferior + 1 na parte superior).
Tem 5 faces (4 faces + 1 de baixo) e 8 lados.
Aplicação das relações de Euler:
p – a + f = 5-8 + 5 = 10-8 = 2
Quarto Poliedro:
Agora temos uma pirâmide pentagonal. Existem seis vértices do gráfico. (na parte inferior + 1 na parte superior).
Também tem 6 lados (5 lados + 1 lado na base) e 10 lados.
Aplicação das relações de Euler:
V – A + F = 6-10 + 6 = 12-10 = 2
Poliedro V:
E finalmente o Pentágono. Se você olhar para a foto, encontrará seis cabeças. (na parte inferior + 2 na parte superior).
Ele também tem 5 faces e 9 arestas.
Aplicação das relações de Euler:
p – a + f = 6 – 9 + 5 = 11 – 9 = 2
Você pode aprender mais sobre poliedros aqui.
………………………………………………………………………………………………………………………………………………..
2.
Completando a tabela, obtemos o primeiro poliedro – V = 8, A = 12, F = 6 e V – A + F = 8-12 + 6 = 2. Segundo poliedro – V = 8, A = 12, F = 6 e V – a + f = 8-12 + 6 = 2; terceiro poliedro – V = 5, A = 8, F = 5 e V – A + F = 5-8 + 5 = 2; 4º Poliedro – V = 6, A = 10, F = 6 e V – A + F = 6-10 + 6 = 2, 5 Poliedro – V = 6, A = 9, F = 5 e V – A + F = 6-9 + 5 = 2.
A relação de Euler é uma fórmula matemática desenvolvida por Leonhard Euler para relacionar as faces, vértices e arestas de um poliedro. A fórmula é V – A + F = 2.
Então, para fazer isso funcionar, se você completar a tabela e aplicar a mesma fórmula aos dados da tabela, você pode obter o resultado 2.
primeiro poliedro
Pico (V): 8
Lado (A): 12
Face (E): 6
V – A + F = 8-12 + 6 = 2
Poliedro II
Pico (V): 8
Lado (A): 12
Face (E): 6
V – A + F = 8-12 + 6 = 2
Poliedro III
Pico (V): 5
Lado (A): 8
Aspecto (P): 5
p – a + f = 5-8 + 5 = 2
4 poliedros
Pico
Lado (A): 10
Face (E): 6
V – A + F = 6-10 + 6 = 2
poliedro v
Pico (V): 6
Lado (A): 9
Aspecto (P): 5
V – A + F = 6-9 + 5 = 2
Em busca de mais informações: