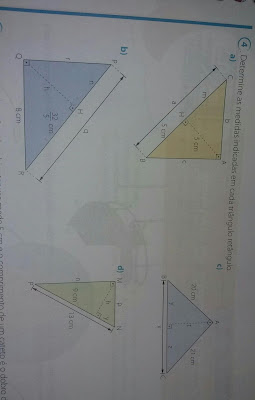
Determine as medidas indicadas em cada triângulo retângulo
Respostas
1.
As medidas indicadas em cada triângulo são:
a) a = 10cm, m = 5 cm, b = , c =
b) q = 10 cm, n = , r = 6 cm, h =
.
c) x = 29cm, h = , z =
cm, y =
, t =
d) y = 4 cm, h = 6 cm, n = , p =
.
Informação útil:
O teorema de Pitágoras é definido por:
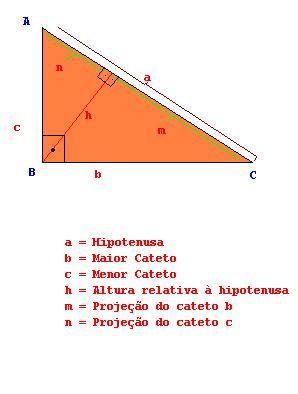
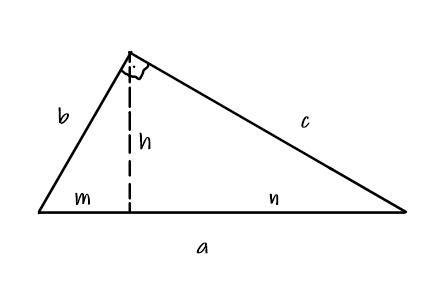
As relações métrica em um triângulo retângulo são:
- a * h = b * c
- b² = m * a
- c² = n * a
- h² = m * n
Onde h é a altura do triângulo, m e n são as medidas resultantes da divisão que o segmento da altura gera na hipotenusa. a representa a hipotenusa, b representa o maior cateto e c representa o menor cateto.
Explicação passo a passo:
a) neste item devemos determinar a medida m, que é parte da hipotenusa, e a medida dos dois catetos do triângulo (b e c). Observando a figura, temos que a altura é h = 5 cm, e a medida n é igual a 5 cm. Assim, temos:
⇒
⇒
Logo, m = 5 cm.
Como a = m + n = 5cm + 5cm = 10cm, podemos determinar b e c fazendo:
⇒
⇒
b) neste item devemos determinar a medida n, que é parte da hipotenusa, a medida do menor cateto do triângulo (c) e a altura h do triângulo. Observando a figura, temos que o maior cateto é b = 8 cm, e a medida m é igual a cm. Assim, temos:
b² = a*m ⇒
Logo a = q = 10 cm. Como a = m + n, temos:
n = a – m =
Logo, n = cm
A altura h do triângulo é:
⇒
⇒
Assim, a altura do triângulo é h = cm.
O cateto menor é:
⇒
⇒
Logo, c = r = 6 cm.
c) Neste item devemos calcular a altura t do triângulo, a medida da hipotenusa x, e as medidas m e n, que agora são, respectivamente, z e y. Observando a figura, temos:
pelo teorema de Pitágoras: ⇒
Assim, a hipotenusa mede x = 29 cm.
A altura t do triângulo é:
⇒
As medidas z e y são:
⇒
⇒
⇒
⇒
d) Neste item devemos calcular a medida y, a medida da altura h, e dos catetos b e c, representados por n e p.
Da relação a = m + n, temos:
13cm = 9 cm + y ⇒ y = 13cm – 9cm = 4 cm
Logo, y = 4 cm.
A altura do triângulo é:
⇒
Assim, h = 6 cm.
Os catetos n e p medem:
⇒
cm
⇒
………………………………………………………………………………………………………………………………………………….