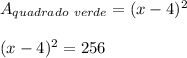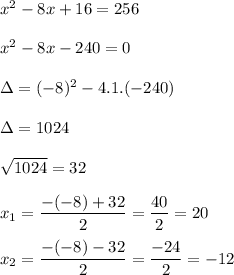02 – Um agricultor rural possui um terreno no formato quadrado e para que ele pudesse movimentar as suas máquinas por todo o terreno, resolveu tirar uma faixa de 4 m na lateral e no fundo do terreno, conforme mostra a figura a seguir. Porém, ele não se lembrava da medida do comprimento e da medida da largura do seu terreno, mas, observou que, após a retirada das duas faixas do terreno, a sua área de plantio passou a medir 256 m². Sendo assim, de quanto era a medida do comprimento original desse terreno antes de ocorrer essa alteração?

a) 12 m.
b) 16 m.
c) 20 m.d) 24 m.

Respostas

1

De acordo com a descrição, a área após a retirada da neve amarela será de 256 metros quadrados, ou seja, a área verde será de 256 metros quadrados. A área de um quadrado é calculada multiplicando a dimensão do lado por 2. Observe o valor frontal da dimensão lateral x conforme mostrado na figura. Em seguida, removemos 4 m de cada borda (parte amarela), para que a borda do quadrado fique verde (x – 4). Agora que conhecemos a área, podemos escrever a equação.

Agora resolva a equação que você fez e encontre o valor de x. Vamos entrar em uma equação quadrática, então precisamos usar a fórmula de Bhaskara

Consegui dois valores para x, mas o problema é com a medição topográfica. As medições topográficas negativas não têm sentido. Assim, com x = 20 m só pode haver uma resposta. mudar

——————————————————————————————————————–

2

Foi referido no comunicado que após a mudança do terreno, a área cultivável (zona verde) passou a ser de 256 metros quadrados.

A área do quadrado é representada por (lados).

x é medido em todo o terreno e é medido a partir do espaço verde de um lado.

X-4.

Em seguida, a área cultivada (área verde) é dada

(x – 4) = 256 → Agora abra este pacote e encontre o valor de x.

(x)² – 2 · x · 4 + (4)²   =   256

x² + 8x + 16  =  256

x² + 8x + 16 – 256 = 0

x² + 8x – 240  = 0     →  Bháskara

a = 1  ,  b = 8  ,  c = – 240

Encontre x = 20 ex = -12.

Como estamos tentando medir a borda da Terra, esse valor não pode ser negativo. Então o valor de x que nos interessa é x = 20.

responda

letra c)

20 metros